手にしたからには、あれこれ触って実態を掴もうとするのが車マニアの性です。で、新しいこの車はどうなのかというと、あまりにも変わり過ぎていて…
最初の印象は「お節介が過ぎる」です。ドアは時速15km/h以上で勝手にロックされますが、この機能は解除できません。同じようにヘッドライトも走っていればオートライト機能が生きてしまい、まだ十二分に明るいのでライトは不要とドライバーが思っても消すことはできません。ライトを消せるのは止まっている時だけ。じっくり観測はしていないのでどの程度の速度でONになるのかはわかりませんが、一旦OFFやスモールポジションにしてもある程度の速度が出たところでオートONになってしまいます。
総じてドイツからの輸入車には同じような傾向が見られますので、ドイツ国内での規制の関係ではないかと思いますね。まぁそこそこ明るい昼間でもライトがONしているのはそのような事情によるので周囲の方には是非ともご理解を賜りたく…
さらにナビ地図の縮尺も勝手に変更されてしまい落ち着きません。7.5時代にインパネ地図は50m、DiscoverPro画面は500m縮尺の設定としていたのですが、8だと両方とも勝手に変わるのでどうにもなりません。というか気付くとどちらも同じ縮尺となってることが多々有りますので、地図をどちらの画面に出すか困ったりもします。
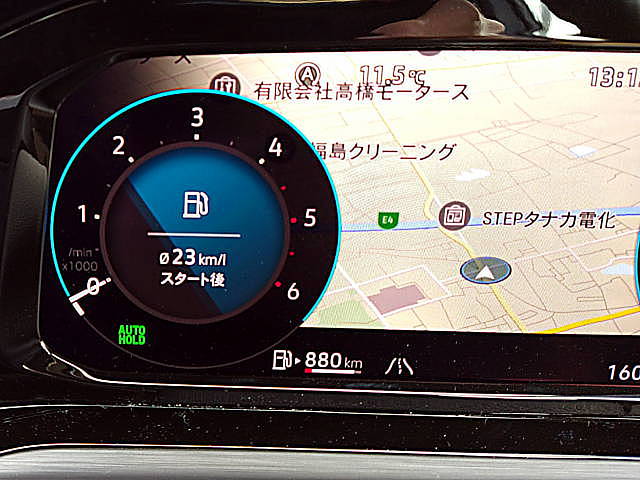
あとは機関系データーがイッキ見できないところかな。こちとらは古い人間なので、機関系のデーター、水温、油温、燃料残、給油後走行距離などは常に監視したいのですが、新しい車では「そんなもん誰も気にしねーよ」と言わんばかりにインパネに表示できません。自動で表示されるのは残走行距離予想だけ.. どうにも落ち着きません。
特にトリップについてはスタンドで「どの程度の金額が必要になるのか」の心構えのためにも欲しいのですが、別項を確認する形でしか内容は掴めません。
新しくなって良くなったところと言うと、まずはオプション装備ではありますがIQ Headlightシステムですかね。Autoでの振る舞いはまだ未体験ですが、ノーマル状態で前車よりかなり明るくなっていて安心できます。
またレーンキープアシストとアダプティブクルーズコントロールが一体化したトラベルアシストですね。カメラの性能がなかなかで、道路脇のラインが塗装(連続or点線)かガードレール等なのか識別して画面に表示しています。また前車の状態を画面に出してくれるのですが、ふらついているとか何方かに寄っているなんてことがすぐに解り面白いですね。
動力系では言うまでもなく新型が圧倒的に良いですね。なにより動き出しが軽く感じるので車が軽くなったように思えます。最大トルク発生回転数が下がって常用域に近づいたことと、トルク自体が20Nm増加しているのがはっきりと効果を発揮しています。またNVHもかなり良くなっていて完全に別格ですね。これには車体の更新の他にタイヤの変更もあるかな。いままではBrigdeStoneのTuranzaという、どちらかと言うとノイズはともかくグリップ重視のタイヤでしたが、新しいこの車ではMichelinのPrimacy4に変更になっていて、タイヤからのノイズがだいぶ減っている印象です。
エンジン音と振動については「ガソリン並」とまでは言いませんが、かなり良くなっているのは事実。車用ディーゼルともガソリンとも違う独特の回転音がして面白いです。
強いて言うなら鉄道用ディーゼルエンジンの音に近いかな。4気筒ではなく6気筒ないしは8気筒エンジンのような音がします。